 打印本文
打印本文  关闭窗口
关闭窗口 3.光纤钟的各种导模
--- 首先分析阶跃折射率光纤中存在哪些模式。对应
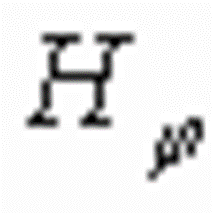 。由波导方程式可知,对于
。由波导方程式可知,对于 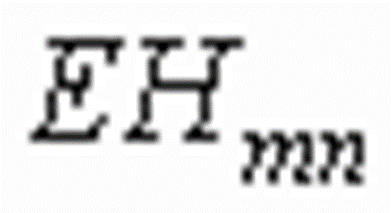 ; 而对于
; 而对于 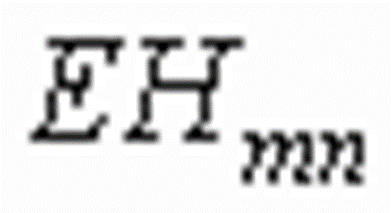 。
。 ---- 当 ![]() 时,
时, ![]() 和
和 ![]() 分量都不为零,为混合模。混合模也分为
分量都不为零,为混合模。混合模也分为 ![]() 和
和 ![]() 两套模式,(2-47)式表示的弱导光纤特征方程。式中“±”表示方程有两组解,取“ ”号为一组解,对应的模式为
两套模式,(2-47)式表示的弱导光纤特征方程。式中“±”表示方程有两组解,取“ ”号为一组解,对应的模式为 ![]() 模;取“-”号为另一组解,对应的模式为
模;取“-”号为另一组解,对应的模式为 ![]() 模。
模。
-- 下面通过弱导光纤特征方程来分析各种模式的截止条件,并求出各种模式的截止频率。
(1) ![]() 模和
模和 ![]() 模
模
--- 令 ![]() ,可得到
,可得到 ![]() 模和
模和 ![]() 模有相同特征方程,为
模有相同特征方程,为
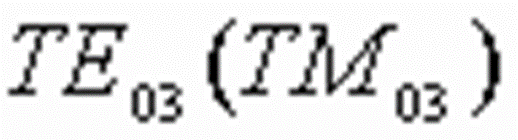 |
(2-48) |
---- 当模式截止时, 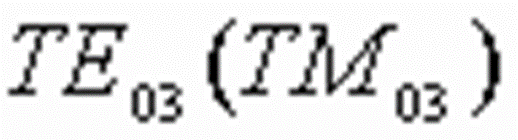 ,
, 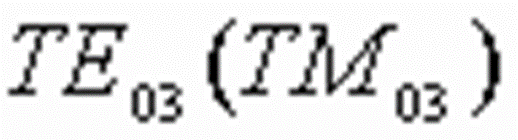 , 由第二类变型的贝塞尔函数的递推关系及渐进公式,可以得到
, 由第二类变型的贝塞尔函数的递推关系及渐进公式,可以得到
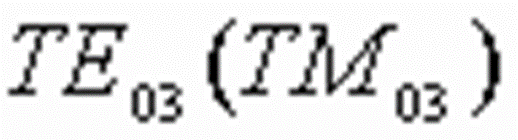 |
(2-49) |
所以截止状态下的特征方程为
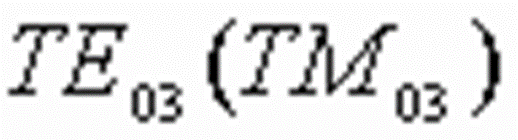 |
(2-50) |
---- 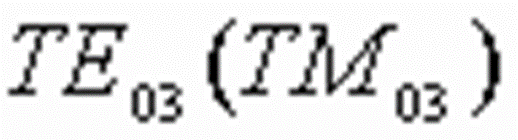 的根有 2.4048, 5.5201, 8.6537,
的根有 2.4048, 5.5201, 8.6537, ![]() ,它们分别对应着
,它们分别对应着 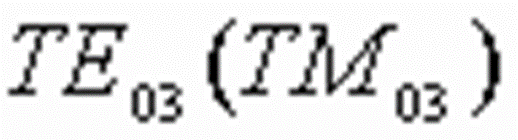 ,
,
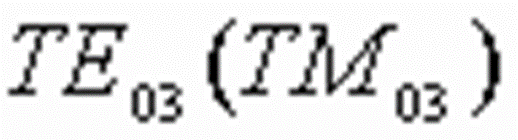 ,
, 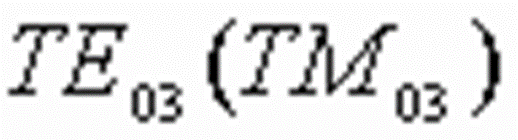 ,
, ![]() 模的截止频率。就是说,若归一化频率
模的截止频率。就是说,若归一化频率 ![]() 2.4048,
2.4048,
则 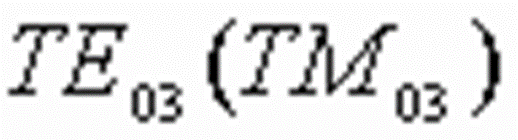 模就能在光纤中存在;反之,若归一化频率
模就能在光纤中存在;反之,若归一化频率 ![]() 2.4048,
2.4048, 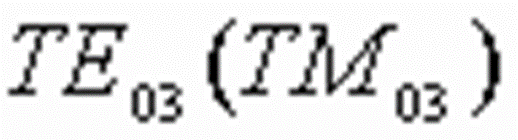 模
模
就不是导模。对其他模式可以次类推。
---- 应该注意, ![]() 和
和 ![]() 模有相同截止频率,它们是相互简并的。
模有相同截止频率,它们是相互简并的。
(2) ![]() 模
模
--- 令 ![]() ,可得到
,可得到 ![]() 模特征方程,为
模特征方程,为
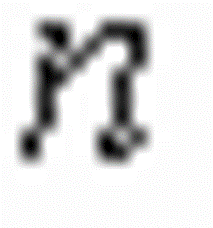 |
(2-51) |
由贝塞尔函数的递推公式将(2-51)式化为
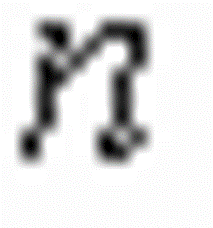 |
(2-52) |
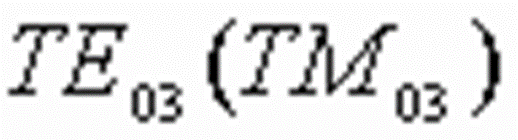 ,可得到
,可得到 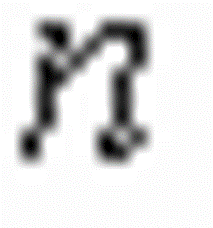 |
(2-52) |
所以截止状态下 ![]() 的特征方程为
的特征方程为
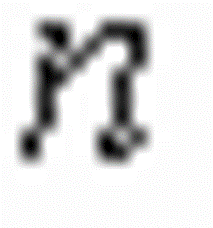 |
(2-53) |
---- 从(2-53) 解出 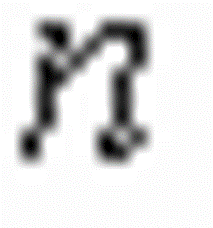 。
。 ![]() 是
是 ![]() 阶贝塞尔函数的第
阶贝塞尔函数的第 ![]() 个根,
个根, ![]() ,对每一个
,对每一个 ![]() ,
,
![]() 的组合,可得到一个相应的
的组合,可得到一个相应的 ![]() 模。
模。
---- 例如,当 ![]() 1时,得到一族
1时,得到一族 ![]() 模,其
模,其 ![]() =
= ![]() =3.8317,7.0156,10.1745,
=3.8317,7.0156,10.1745, ![]() ,其他可以次类推。
,其他可以次类推。
(3) ![]() 模
模
--- 令 ![]() ,可得到
,可得到 ![]() 模特征方程,为
模特征方程,为
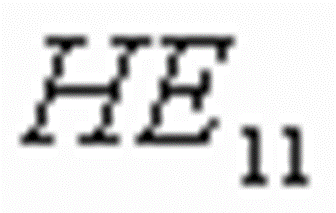 |
(2-54) |
由贝塞尔函数的递推公式将(2-54)式化为
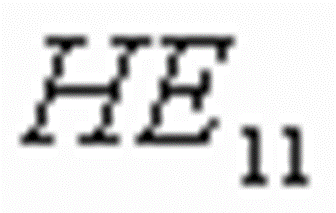 |
(2-55) |
分 ![]() ,
, ![]() 两种情况进行讨论。
两种情况进行讨论。
----- <1> 当 ![]() 时,截止状态下
时,截止状态下 ![]() 的特征方程为
的特征方程为
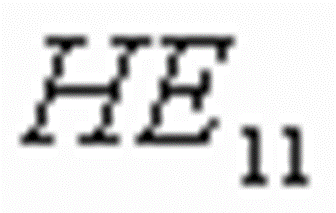 |
(2-56) |
| 所以 | 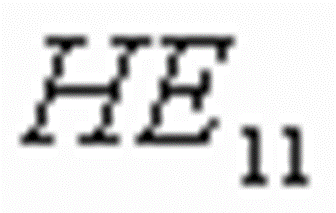 |
(2-57) |
----
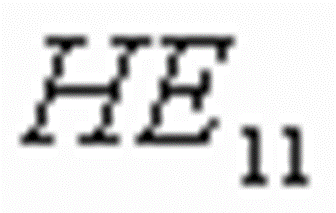 的根有 0,3.8317 ,7.0160 ,10.1735,
的根有 0,3.8317 ,7.0160 ,10.1735, 即截止波长为无穷大。
模,是单模光纤的工作模。
----- <2> 当 ![]() 时,截止状态下
时,截止状态下 ![]() 的特征方程整理后为
的特征方程整理后为
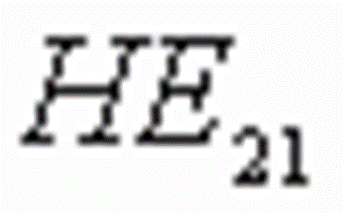 |
(2-58) |
| 得到 | 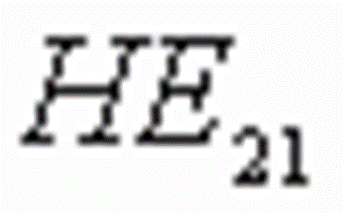 |
(2-59) |
---- 例如,当 ![]() 2时,
2时, 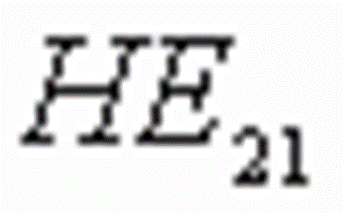 的根有 2.4048, 5.5201, 8.6537,
的根有 2.4048, 5.5201, 8.6537, ![]() ,它们分别对应着,
,它们分别对应着, ![]() ,
, ![]() ,
, ![]() 模,
模, ![]() 模在截止时与
模在截止时与 ![]() 、
、 ![]() 简并。
简并。
---- 表2-1给出几个较低阶贝塞尔函数的前几个根。
表2-1 贝塞尔函数的前几个根
| 贝塞尔函数 | |||
|
2.40483 | 3.83171 | 5.13562 |
| 5.52008 | 7.01559 | 8.41724 | |
| 8.65373 | 10.17347 | 11.61984 |
--- 从以上分析可以知道,
中传输,它的截止频率为零。如果光纤的归一化频率
式还没有出现时,光纤只有
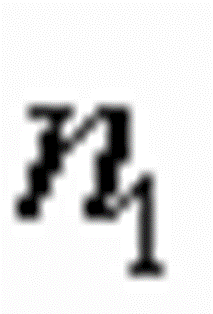 |
||
| 或 | 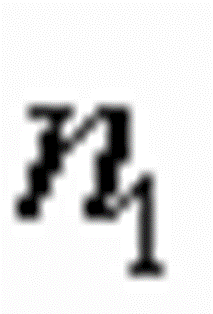 |
(2-60) |
式中, ![]() 为纤芯半径,
为纤芯半径, ![]() 为纤芯的折射率,
为纤芯的折射率, ![]() 为包层的折射率,
为包层的折射率, ![]() 为工作光波长。
为工作光波长。
(2-60)式就是 阶跃折射率光纤单模传输的条件 。
(4) 远离截止时的 ![]() 和
和 ![]() 模
模
-- 当 W→∞,U→0是模式远离截止的条件。可得到远离截止 ![]() 和
和 ![]() 模的特征方程为
模的特征方程为
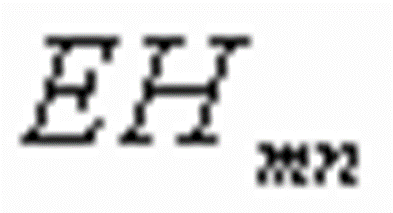 0 0 |
(2-61) | ||
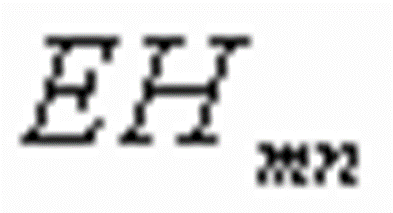 0 0 |
(2-62) |
 打印本文
打印本文  关闭窗口
关闭窗口