|
(武汉大学 电子信息学院,湖北 武汉430079)
摘 要:为了在既定尺寸下减小斜坡波导和弯曲波导的功耗,设计了4种过渡
波导形状函数,用有限差分光束传播法(FD-BPM)进行了模拟分析,发现过渡波导形状的选 取与坡度和曲折角存在条件关系,并给出了条件表达式和详细说明.
关键词: 光波导;有限差分光束传播法;集成光学
随着光电子产业的迅速发展,越来越多的有源及无源光子、光电子器件趋于集成化,这些器
件往往有复杂的光波导结构,很难有具体的解析解.因而,用快速精确的数值模拟来作为器
件的理论依据就愈加显得重要.1989年KochTB[1]等首先提出了基于Helmholtz方程
的有限差分解法,该方法快速简单而且精确,是目前较为优越的光波导器件分析算法.
斜坡波导和弯曲波导是集成光电子器件中两种重要的过渡器件单元.斜坡波导用于连接两个
中心轴重合而宽度不同的直波导,相关文献极少,是本文讨论的重点;弯曲波导用于连接两
个宽度相同且中心轴平行的直波导.以前计算弯曲波导损耗的方法有Macatili和Miller发展
的“速率法”[2],也有文献用FFT-BPM法对它进行了计算[3].由于这两 种波导都是动态单元,对于它们的分析不可能如同简单的平面波导一样进行本征分析,光
在其中传播是动态的而非固定本征的,所以在本文中将使用有限差分光束传播法(FD-BPM) [4]来进行分析.
通过分析可以看出该方法用于分析动态波导的优越性,其结果对于实际工程中进行相关波导 的优化设计具有重要的参考价值.
1 FD-BPM的原理
φ(x,z)exp(-iwt)形式下的单色波,对二维波导,可写成标量波方程
z)φ=0.其中,z为波导传播方向;ω为光的角频率;n(x,z)是介质折射率,令φ(x
,z)=u(x,z)exp(ikrz),kr为任意常数,要求它的选择使u(x,z)是z的缓变函数,把 此式代入波动方程,忽略φ2
依赖于空间坐标的波数,离散u(x,z)(记为u(xs,zr))横向节点为xs=a+s× Δx;s=0,…,N;Δx=(b-a)/N;横向窗口范围为
(a,b);Δx为节距;N+1为节点总数;纵向(波导传播方向)节点位于zr=r×Δz;r =0,1,…;Δz为纵向步长.
在众多的差分格式中,选择绝对稳定的CrankNicholson格式[5]的修改格式,关
于半步长点(s,r+1/2)作差分近似,因为公式完全等同于文献,这里不再列出.对于
边界条件的选取,为了防止在计算窗口的边界引起反射,我们使用TBC[6]边界条件 .
2 过渡波导的BPM法分析
2.1 斜坡波导
斜坡波导是连接两不同宽度直波导的过渡单元,为了在既定尺寸下减小其功耗,我们设计了
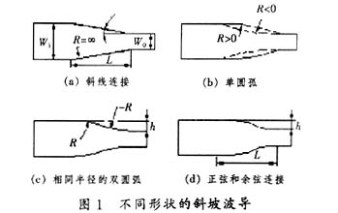
几种有可能减小功耗的波导形状,如图1所示.通过比较分析,得出了最佳的斜坡波导及其使 用条件.
在图1中,Wi为斜坡波导入口端直波导宽度;Wo为出口端直波导宽度;L是
斜坡波导长度;h=(Wi、Wo)/2是斜坡高度;R是圆弧曲率半径.经分析可知,一旦
确定图1(a)中的Wi、Wo和L,则图1(c)、(d)的形状就可以唯一确定,而
图1(b)未定,它可以用无数个不同曲率半径的圆弧进行连接,这些圆弧分别对应有不同的功
耗,因此我们先进行单圆弧斜坡波导的功耗分析.我们规定凸圆弧的曲率半径>0,凹圆弧的 曲率半径<0,斜线的曲率半径为无穷大.

在FD-BPM运算中将采用的参数:计算窗口300μm,差分网格数1000,直波导中计算步
长5μm,过渡波导中的步长0.5μm.对于光波导的参数,为了加大斜坡波导坡度的变
化范围,我们采用大宽度的单模波导,波导区的折射率为1.01,光限制层的折射率为1,真
空中波长6.28μm.斜坡形状参数,入口端宽度Wi=20μm,出口端宽度Wo 不定,用来改变斜坡的坡度α,斜坡长度L=0.1mm.由于斜坡波导的功耗与坡度直接
有关,所以,我们计算了6个不同出口端宽度下的曲率半径与功耗的关系图,结果如图2(a
)~(f)所示.各图所对应的出口端宽度分别为6、8、10、12、15和18μm,由于当曲率
半径R>20mm的功耗变化很小,基本接近于斜线连接的情况,所以R=20mm处用 斜线连接的功耗来代替.
由图可见,功耗随出口端宽度的增大而减小,负曲率半径对应的功耗都比较大.正曲率半径
部分的曲线都是先快速递减然后递增,因此存在一个最小功耗的曲率半径,我们称该半径为
最佳曲率半径.当圆弧半径小于最佳曲率半径时,功耗会陡增,反之,功耗随曲率半径的增 加而缓慢增长;当半径超过20
mm后其功耗基本不变,与斜线连接对应的功耗相等.所以 在使用单圆弧连接时,其曲率半径应该等于或略大于最佳曲率半径,一定不能取的过小.比
较图2(a)~(c)和(d)~(f),我们还可以看出随着出口端宽度的增加,其递增曲线变的平缓,
说明大坡度的斜坡采取圆弧过渡效果比小坡度的更明显,如表1所示.由表1我们可以发现,
当Wo>15即坡度角α<arctan(0.025)时,用圆弧优化的效果不明显, 可以用斜线直接连接.

下面我们分析另外3种形状的斜坡波导:双圆弧R=(L2/4h+h/4)、正弦x(z)=hz/L-(h/2
π)sin(2πz/L)和余弦x(z)=h[1-cos(πz/L)]/2.为了跟单圆弧波导有个
比较,我们加进了斜线连接的情况,计算结果如图3(a)~(d)所示.当斜坡长度L和出口
端宽度Wo都比较大即坡度很小的情况下,采用双圆弧连接功耗最小,正弦曲线不能达 到减小功耗的效果.从图3中我们还发现,双圆弧功耗曲线与斜线功耗曲线存在一交点,该点
所对应的出口端宽度我们称为临界宽度,其坡度为临界坡度.当出口端宽度大于临界宽度时 ,可以采用双圆弧斜坡来减小功耗.通过大量计算我们发现,使用双圆弧的条件为Wo
>20-0.006 L,其结果验证如表2所示.从表2中我们可以看到由20-0.006L计算出来的值都略
大于或接近临界出口宽度.因此当斜坡出口宽度Wo>20-0.006 L时采用双圆弧连接的 功耗最小.当Wo<20-0.006
L时应采用单凸圆弧连接,其曲率半径应等于或略大于最 佳曲率半径.


2.2 弯曲波导
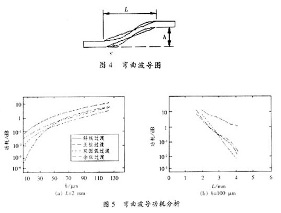
连接两平行直波导的弯曲波导如图4所示.对于一定的h值,要求尽可能缩短L,并且连接损
耗越小越好.下面我们同样采用斜线、正弦、余弦和双圆弧4种弯曲波导的线型来 进行比较分析.取波导参
数:波导宽度方向x的折射率分布n(x)=2.1512+0.0035cosh- 2(2x/W),波导中心为x零点,波导宽度W=6μm,真空光波长λ=1.3μm,可
以验证,该波导为单模波导.FD-BPM计算参数不变.计算结果如图5(a)和(b)所示.从图中
我们可以看到当曲折角h/L<1/40时,采用正弦曲线功耗最小,当h/L>40时,用余弦曲 线连接功耗最小.

3 总结
我们用FD-BPM模拟分析了斜坡波导和弯曲波导的传输过程.其中我们设计了4种线型函
数,作了功耗比较分析,发现过渡波导形状的选取与坡度和曲折角有很大关系,并给出了表
达式.对于斜坡波导,在短距离和大坡度条件下应该考虑选用正曲率半径的单圆弧连接,但
半径不能太小;大斜坡长度和小坡度条件下应该用双圆弧过渡.弯曲波导的形状函数也应该 根据曲折角来选取优化.
参考文献
[1]Koch T B,Davies J B,Wichkramasinghe D.Finite element/finite diffe rence
propagation algorithm for integrated optical device [J]. Electronics Let
ters,1989,25(6):414-516.
[2]Marcatili E A,Miller S E.Improved relations decribing directional contr
ol in eletrom genetic wave guidance [J]. Bellsyst.Tech.J.,1969,48(9):2161-21 88.
[3]严朝军,许政权,陈益新.确定一维单模波导特性的差分波束传输法 [J].上海交通 大学学报,1996,31(7):73-76.
[4]陆金甫,顾丽珍,陈景良.偏微分方程差分解法 [M].北京:高等教育出版社,1988.
[5]Hadley G R. Transparent boundary condition for beam propagation [J]. Op
t. Lett.,1991,16:624-626.
|
