光纤的波动理论
5.光纤中的模式传输 --- 由光纤的参数及工作波长计算出归一化频率V后,从图-14中就可以判断光纤中可能存在几种模式传输。
图-14 导模传输条件
2.3.3 近似解-LP模
---- 由于矢量模的求解繁琐, 对于大多数的实际光纤都采用近似解, 最常用的近似方法
是标量近似法(用于阶跃光纤)及 WKM 近似法(用于渐变光纤)。 标量近似法是指在弱导波
光纤中, 将光纤的横向电场和横向磁场当作标量处理, 所得到的导波模式称为线性偏振
模,用 LPmn "Linearly Po1arized(LP)modes" 表示。
1 特征方程
--- 在近似模式理论基础上,可得到标量的亥姆霍兹方程,写到圆柱坐标系中,可得到
|
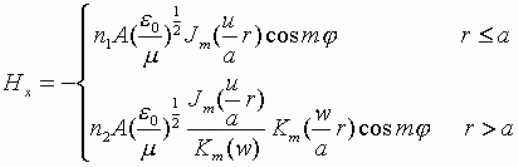 |
(2-63) |
求解(2-63)式,通过变换得到直角坐标系中的横向场分量为
|
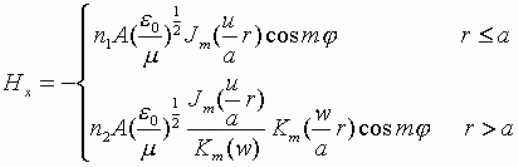 |
(2-64) |
|
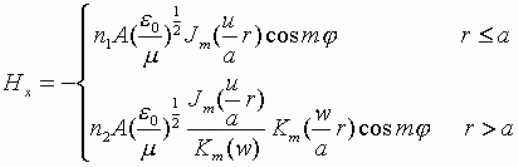 |
(2-65) |
由电磁场的边界条件,可以确定出 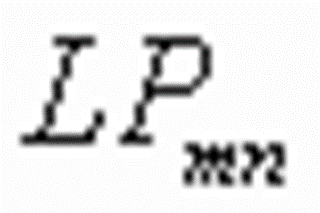 模的特征方程为 模的特征方程为
|
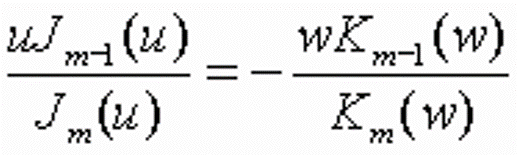 |
(2-66) |
2 线性偏振模及其特性
---- 当模式截止,  时,利用第二类变型的贝塞尔函数渐进公式,由(2-66)式可得到 时,利用第二类变型的贝塞尔函数渐进公式,由(2-66)式可得到
|
 |
(2-67) |
所以,截止状态下 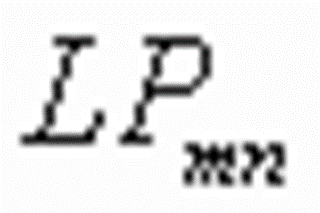 特征方程为 特征方程为
|
 |
(2-68) |
也就是说, 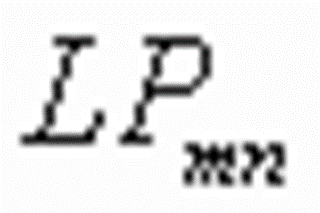 模的归一化截止频率 模的归一化截止频率  由 由  来确定。 来确定。
---- 求出各种LPmn模的归一化截止频率  。 因此, 当进入光纤中的信号归一化频率 。 因此, 当进入光纤中的信号归一化频率  大于某种模式的截止频率 大于某种模式的截止频率  时,该信号可在光纤中传输;反之,若 时,该信号可在光纤中传输;反之,若  ,则与 ,则与  相应的模式将被截止,不能在光纤中传输。 相应的模式将被截止,不能在光纤中传输。
---- 对于远离截止时的传输特性,其特征值 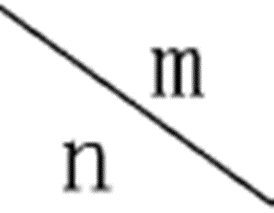 随归一化频率 随归一化频率  而变化,因此远离截止时的 而变化,因此远离截止时的
特征方程可简化为Jm(u)=0,从而 。远离截止时的特征方程 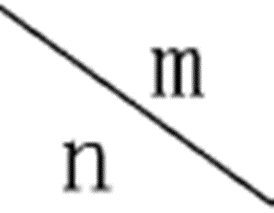 等于m阶贝塞尔函数的第n个 等于m阶贝塞尔函数的第n个
根 。表2-2给出了光纤中几个低次 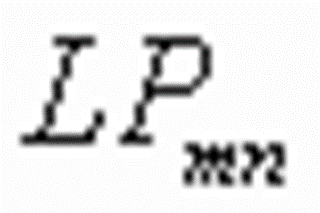 模截止时的 模截止时的 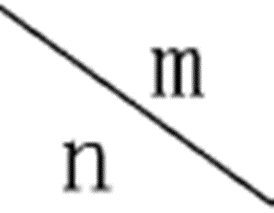 值和远离截止时的 值和远离截止时的 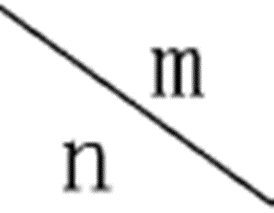 值 值
----- 表2-2 -- 几种 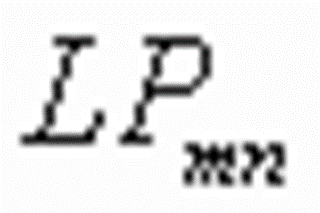 模的 模的  值和 值和  值 值
|
