光纤的波动理论
2. 圆柱坐标系中的波动方程
--- 均匀波导中纵向场 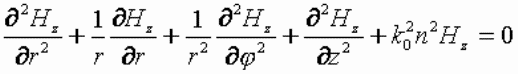 、 、 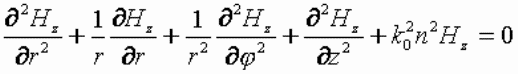 的波动方程为: 的波动方程为:
|
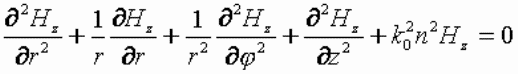 |
(2-26) |
|
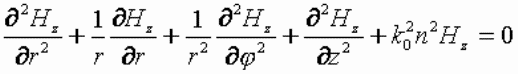 |
(2-27) |
--- 在圆柱坐标系中纵向场 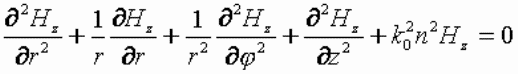 、 、 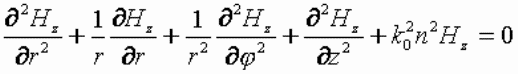 的波动方程表示为: 的波动方程表示为:
|
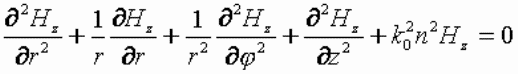 |
(2-28) |
|
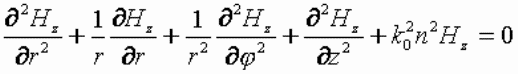 |
(2-29) |
式中: 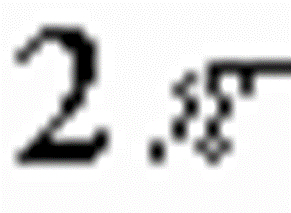 为自由空间的波数; 为自由空间的波数; 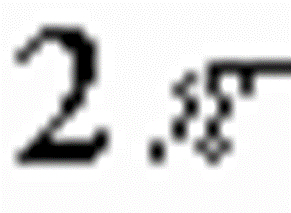 ; ; 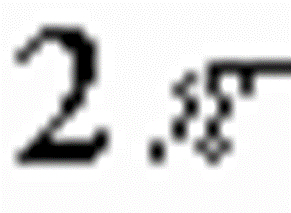 为介质的折射率。 为介质的折射率。
- 其中, 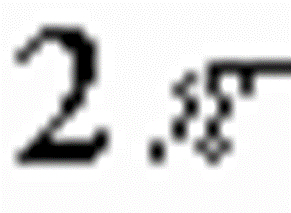
2.3.2 阶跃折射率光纤中波动方程的解
---- 用分离变量法求解式(2-28)和式(2-29) 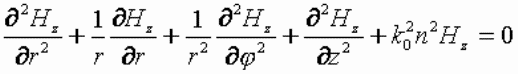 、 、 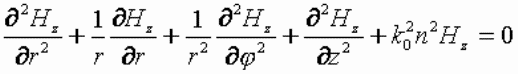 波动方程,令 波动方程,令
|
 |
(2-30) |
|
 |
(2-31) |
--- 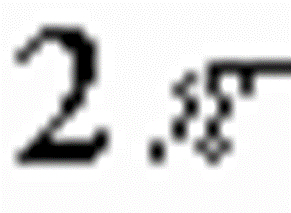 表示导波沿光纤轴向的变化规律应为行波,用表示其传播的相位常数,则 表示导波沿光纤轴向的变化规律应为行波,用表示其传播的相位常数,则
|
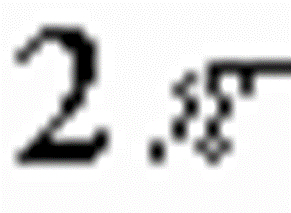 |
(2-32) |
---- 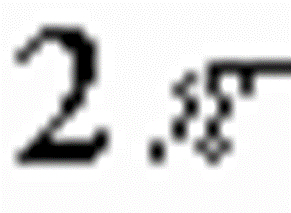 表示沿 表示沿 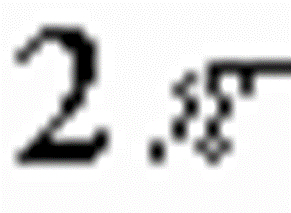 方向(圆周方向)的变化规律应是以 方向(圆周方向)的变化规律应是以 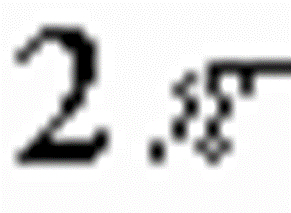 为周期的函数,则 为周期的函数,则
|
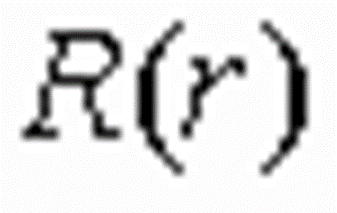 |
m=0,1,2,... |
(2-33) |
由式(2-28)~(2-33),可得:
|
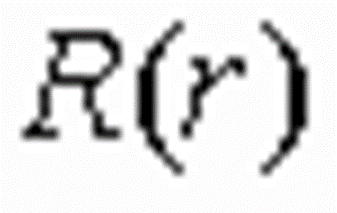 |
(2-34) |
---- 上式(2-34)是贝塞尔方程,在特定的边界条件下求解 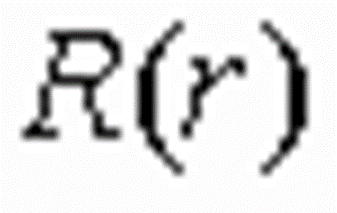 ,便可得到阶跃折射率光 ,便可得到阶跃折射率光
纤的模式情况。
1.解 的形式
--- 求解方程(2-34)式的过程,实际上就是根据边界条件选择适当的贝塞尔函数的过程。
(1) 在纤芯中( 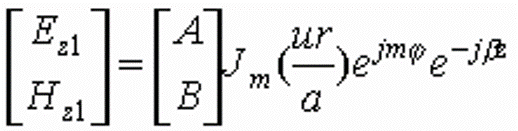 ), ), 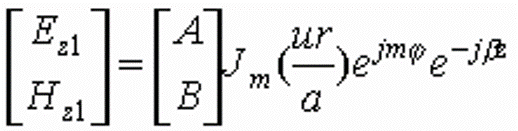
--- 对于传输导模,在纤芯中沿径向应呈驻波分布,方程(2-34)式应有振荡形式的解。为
此,应满足 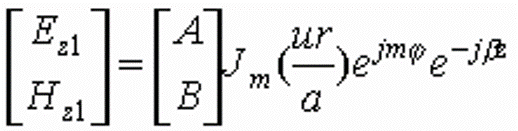 的条件。同时,纤芯包含了r=0的点,在这一点,光场分量应为 的条件。同时,纤芯包含了r=0的点,在这一点,光场分量应为
有限值,所以只能采用第一类贝塞尔函数 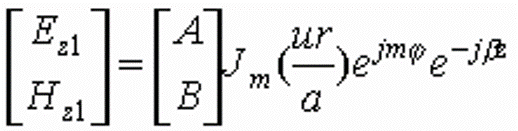 ,令 ,令
|
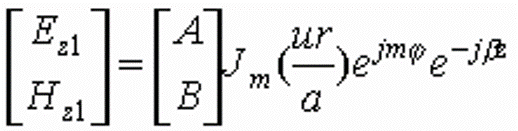 |
(2-35) |
可得到
|
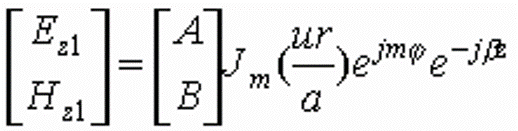 |
(2-36) |
式(2-36)中:A,B为常系数。
(2) 在包层里( 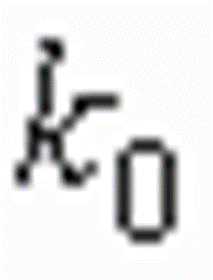 ), ), 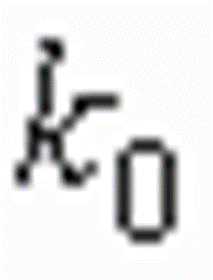
---- 对于传输导模,在包层里场分量应迅速衰减,因此,应满足 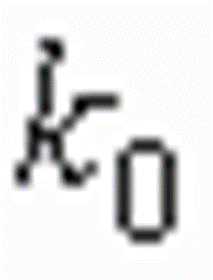 的条件。 的条件。
才能得到变型贝塞尔方程的解。此外,包层包括无穷远处,所以不能采用第一类贝塞尔函
数,而只能用第二类变型的贝塞尔函数 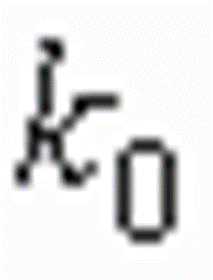 。令 。令
|
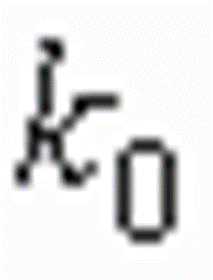 |
(2-37) |
可得到
|
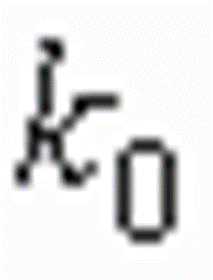 |
(2-38) |
式(2-38)中:C,D为常系数。
--- 结合参量 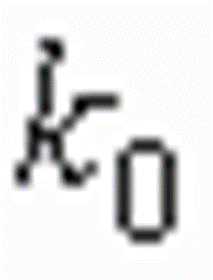 和 和 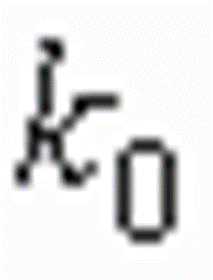 ,可以定义光纤的重要的结构参量 ,可以定义光纤的重要的结构参量 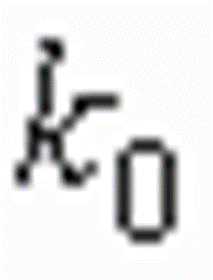 为 为
|
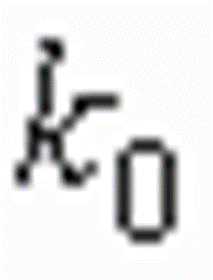 |
(2-39) |
---- 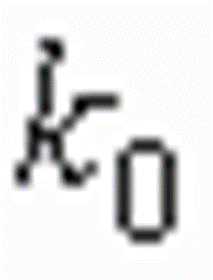 一方面与波导尺寸(芯径a)成正比, 另一方面又与真空中的波数 一方面与波导尺寸(芯径a)成正比, 另一方面又与真空中的波数 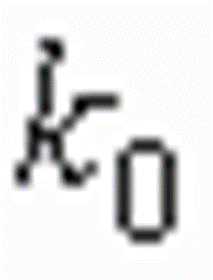 成正比,而 成正比,而  (c为真空中的光速),因此 (c为真空中的光速),因此 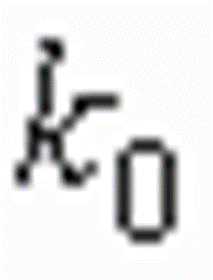 称为光纤的归一化频率。 称为光纤的归一化频率。 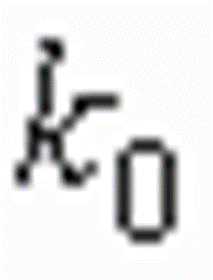 是决定光纤中模式数量 是决定光纤中模式数量
的重要参数。
---- 从以上的求解过程也可以的得出导模的传输条件。为了得到纤芯里振荡、包层里迅速
衰减的解的形式,必须满足:
|
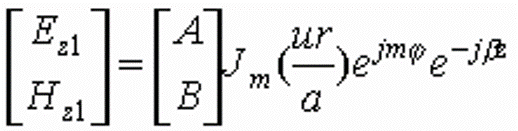 和 和 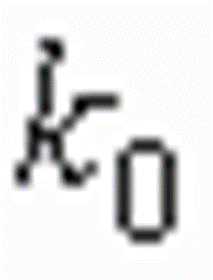 |
(2-40) |
因此,导模的传输常数的取值范围为:
|
 |
(2-41) |
----- 若  ,则 ,则  , 这时包层里也得到振荡形式的解, 这种模称为辐射模。 , 这时包层里也得到振荡形式的解, 这种模称为辐射模。
 表示一种临界状态,成为模式截止状态,模式截止时的一些性质往往通过 表示一种临界状态,成为模式截止状态,模式截止时的一些性质往往通过 
时的特征方程式来讨论。
---- 相反地,  或 或  的情况是一种远离截止的情况,模式远离截止时其电磁场 的情况是一种远离截止的情况,模式远离截止时其电磁场
能量 很好地封闭在纤芯中。
|
